1
Y=x^24x5 juddjungle juddjungle 3 weeks ago Mathematics High School answered Y=x^24x5 what is the vertex, domain, and range?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
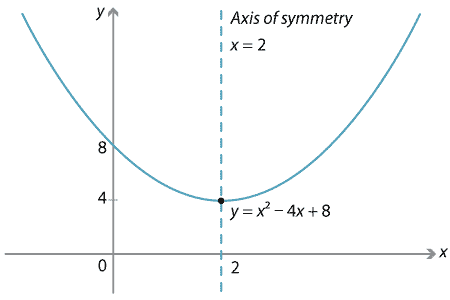
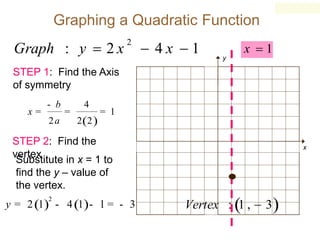
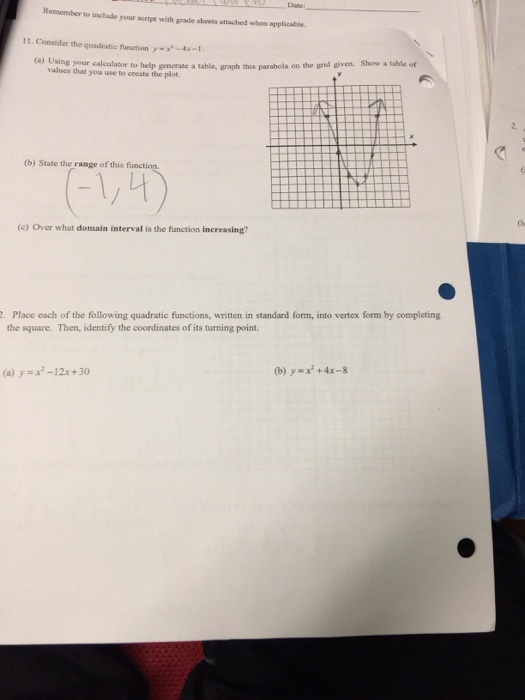
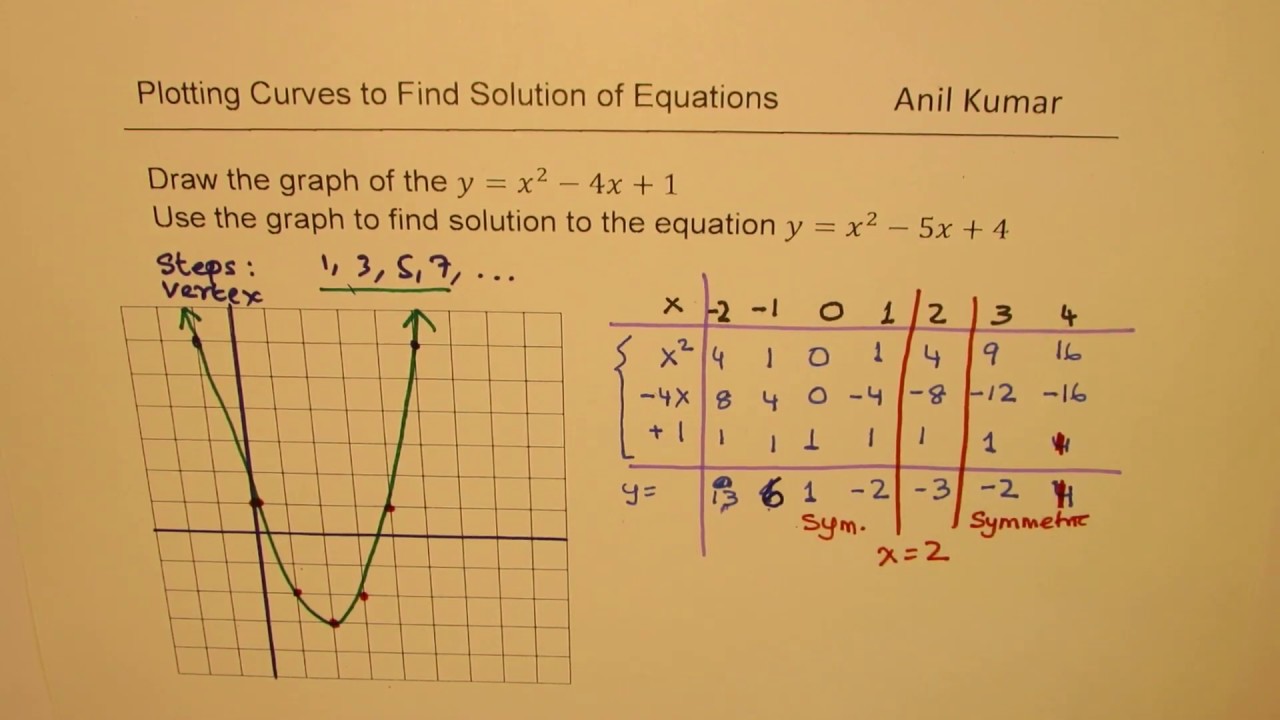
Find the vertex of y=x^2-4x-1
Find the vertex of y=x^2-4x-1-X 2 − 4 x 1 = y Subtract y from both sides Subtract y from both sides x^ {2}4x1y=0 x 2 − 4 x 1 − y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 4 for b, and 1y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}Solve Study Textbooks Guides Join / Login Question The vertex of the parabola x 2 y 2 The vertex of the parabola 4 y 2 1 2 x − 1 2 y 3 9 = 0 is Hard View solution >

Changing Quadratic Functions From Standard Form To Vertex Form Flashcards Quizlet
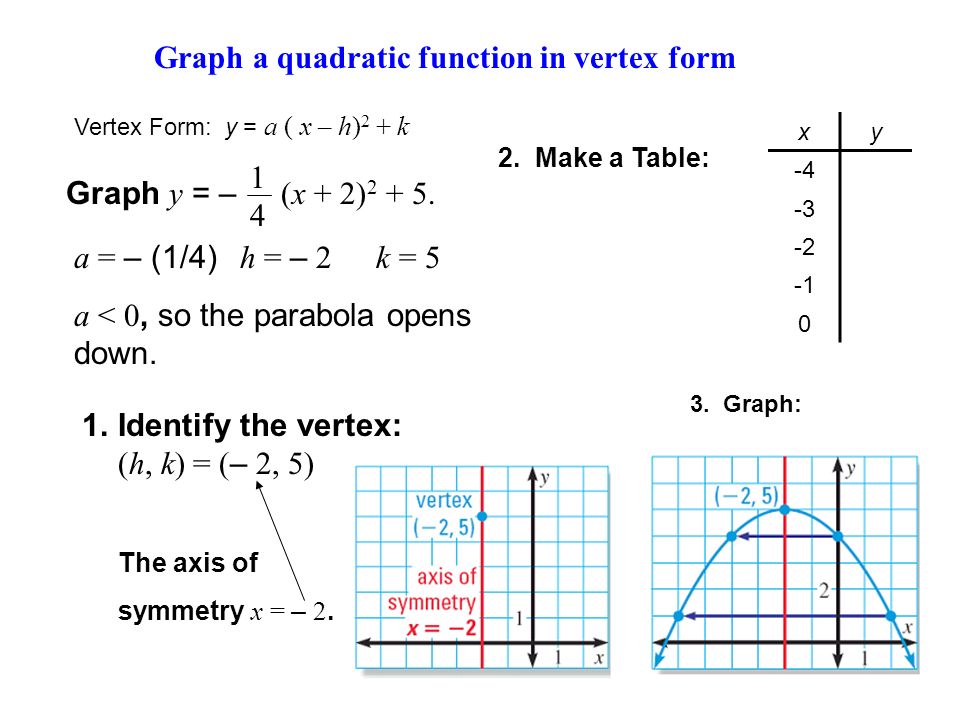
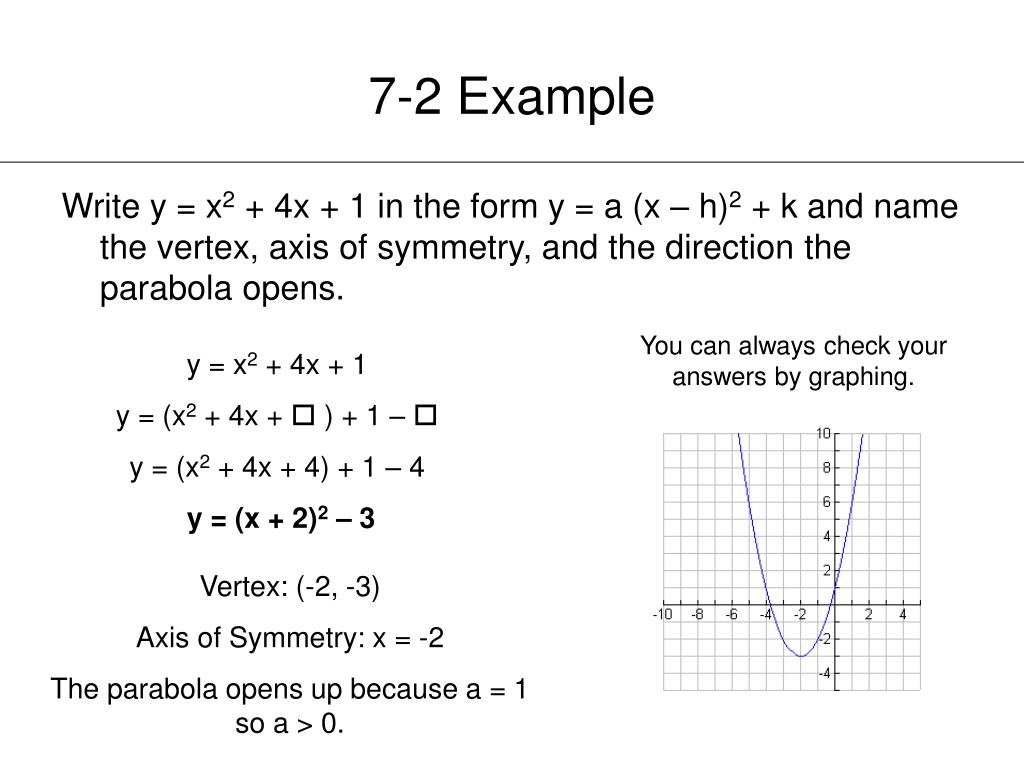
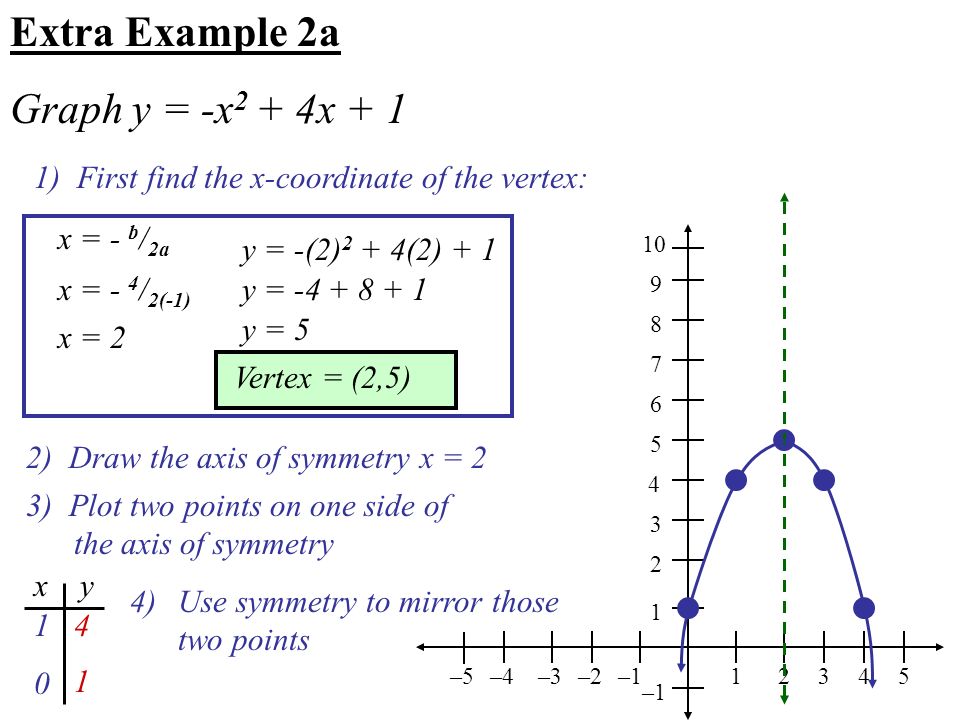
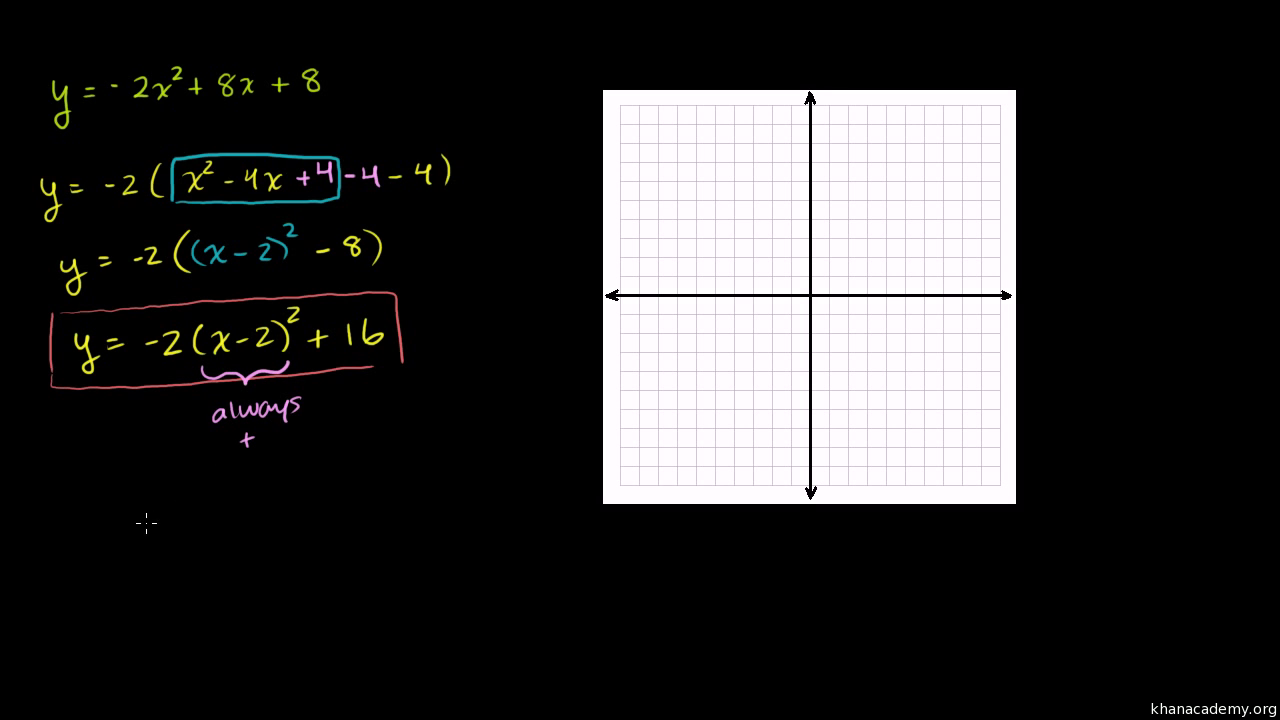
y= A(xh)^2k Since you have a MONIC polynomial (leading coefficient, of x^2 is 1), A=1 in the formula above The beauty of writing a quadratic or parabola this way, is that the vertex (the minimum y value if A>0;Y=x^24x2 Your questions can be answered after we change equation to standard form y=(xh)^2k, with (h,k) being the (x,y) coordinates of the vertex completing the square to convert to standard form, y=(x^24x4)24 y=(x2)^26 This parabola opens downward because the coefficient of x^2 is negative If the coefficient is positive, itYou can find the vertex from both standard and vertex forms manually But the fastest mean will be the vertex form converter To learn how to calculate the vertex, keep reading Through standard form The standard form of a quadratic equation is ax 2 bx c There are two formulas that are used to find the x and y
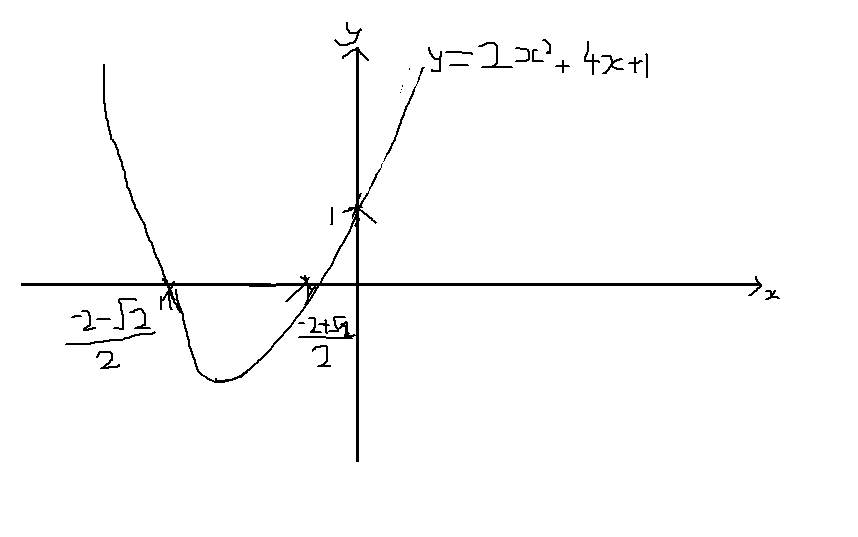
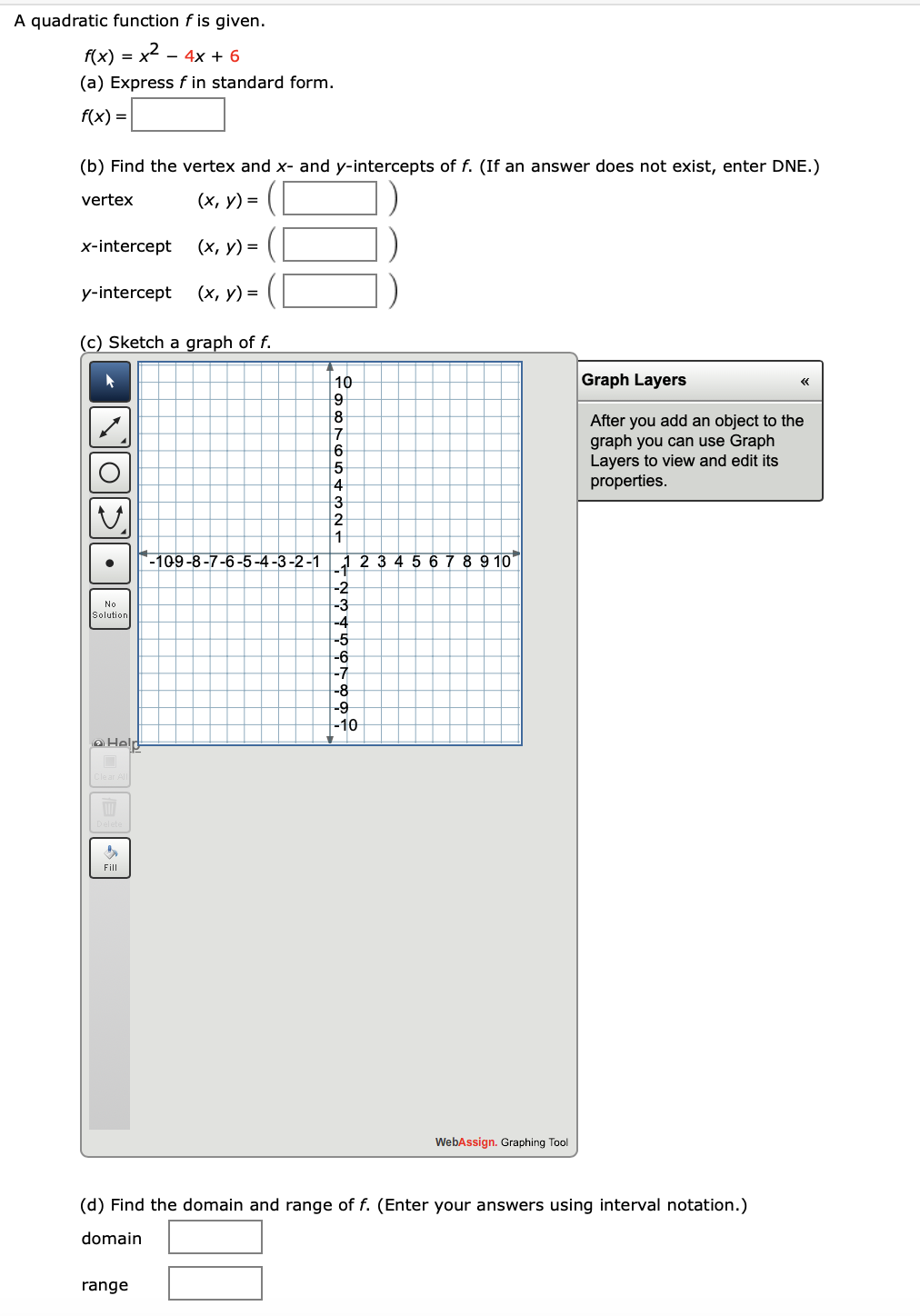
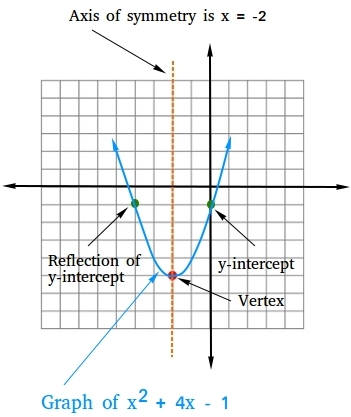
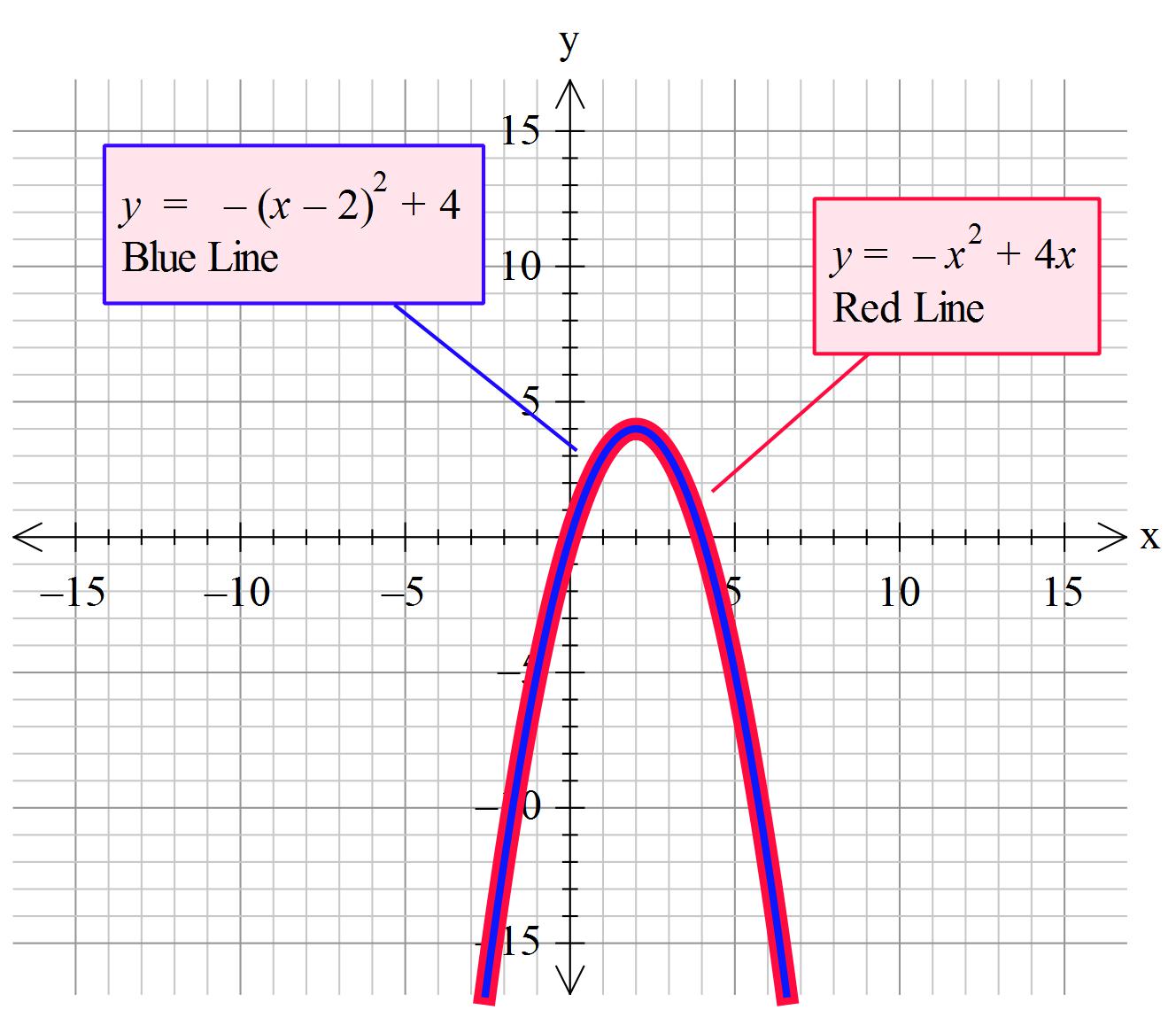
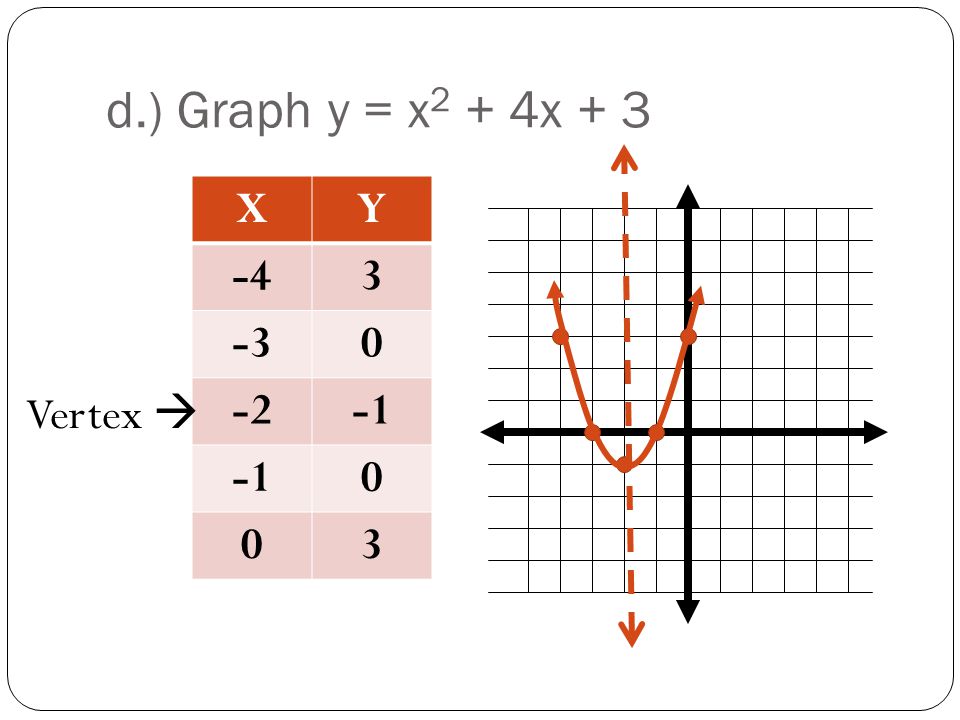
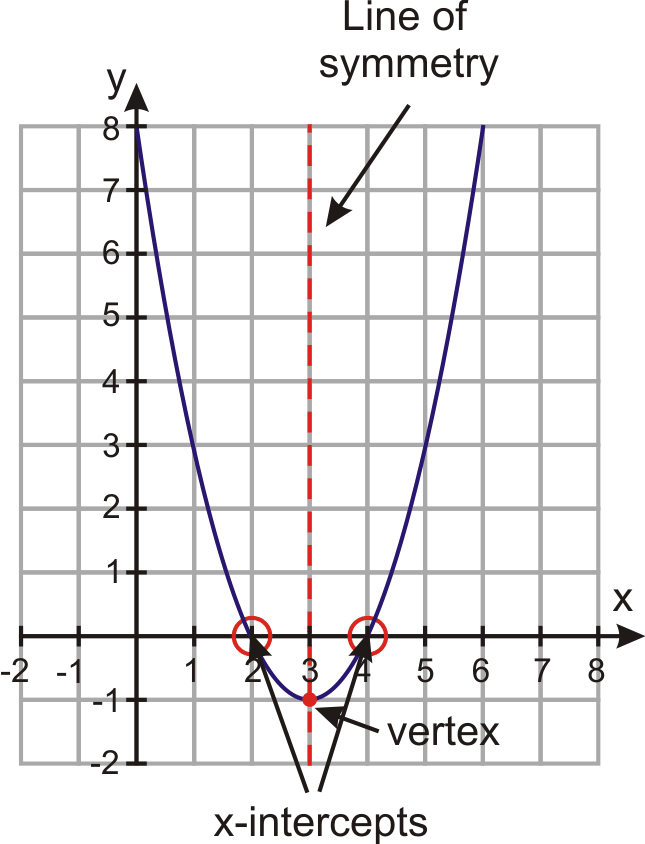
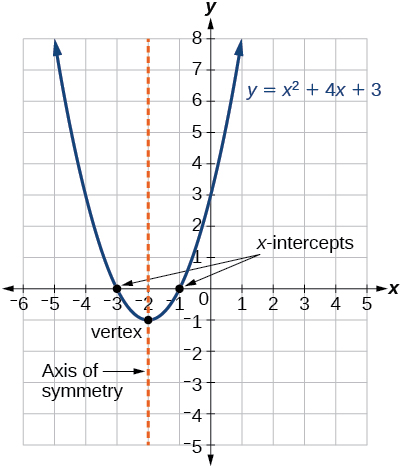
The equation of a parabola is 12y=(x1)^248 Identify the vertex, focus, and directrix of the parabola Algebra The vertex of a parabola represented by f(x)=x^24x3 has coordinates of (2,1) Find the coordinates of the vertex of the parabola defined by g(x)=f(x2) Explain how you arrived to your answerClick here👆to get an answer to your question ️ The vertex of the parabola x^2 y^2 2xy 4x 4y 4 = 0 is at? since this is a parabola with x being quadratic and y being linear then we'll have y = x² 4x 1 multiplying both sides of the equation with 1 y = x² 4x 1 transposing 1 to the left side y 1 = x² 4x or x² 4x = y 1 complete the square for x by adding 4 to both sides of the equation x² 4x 4 = y 1 4
Find the vertex of y=x^2-4x-1のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
/1000px-Parabola_features-58fc9dfd5f9b581d595b886e.png) |  | |
 |  | |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | .gif) |  |
 |  | |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Find the vertex of y=x^2-4x-1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
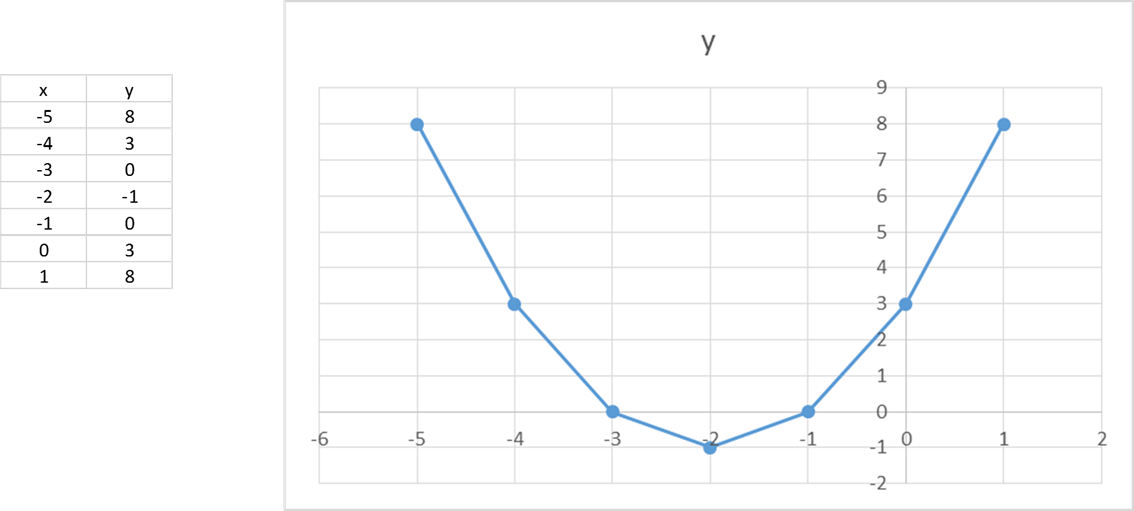 |  |
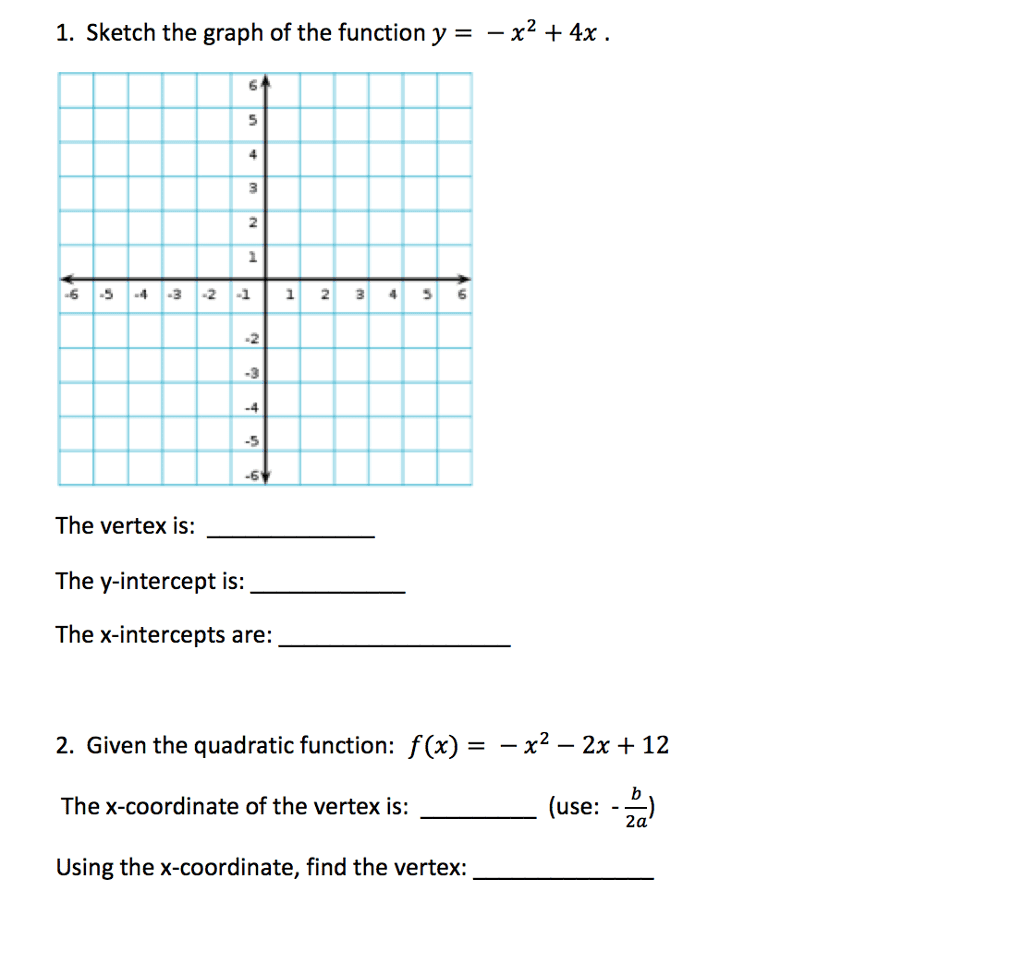
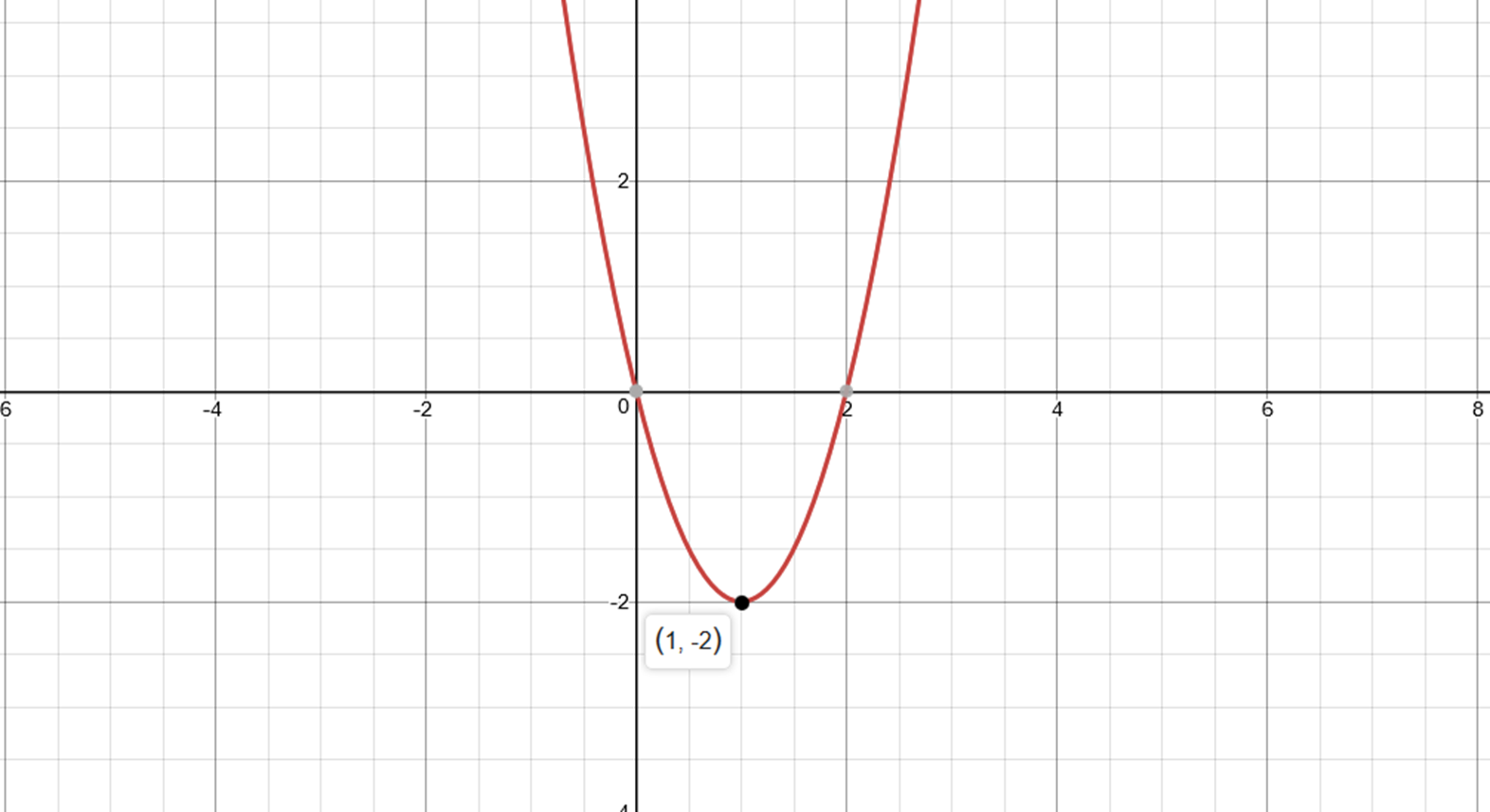
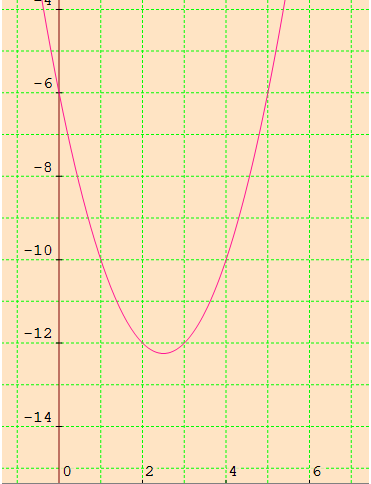
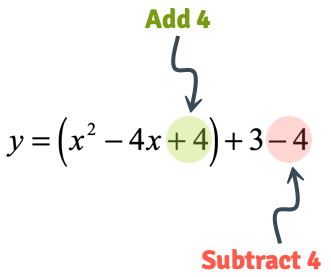
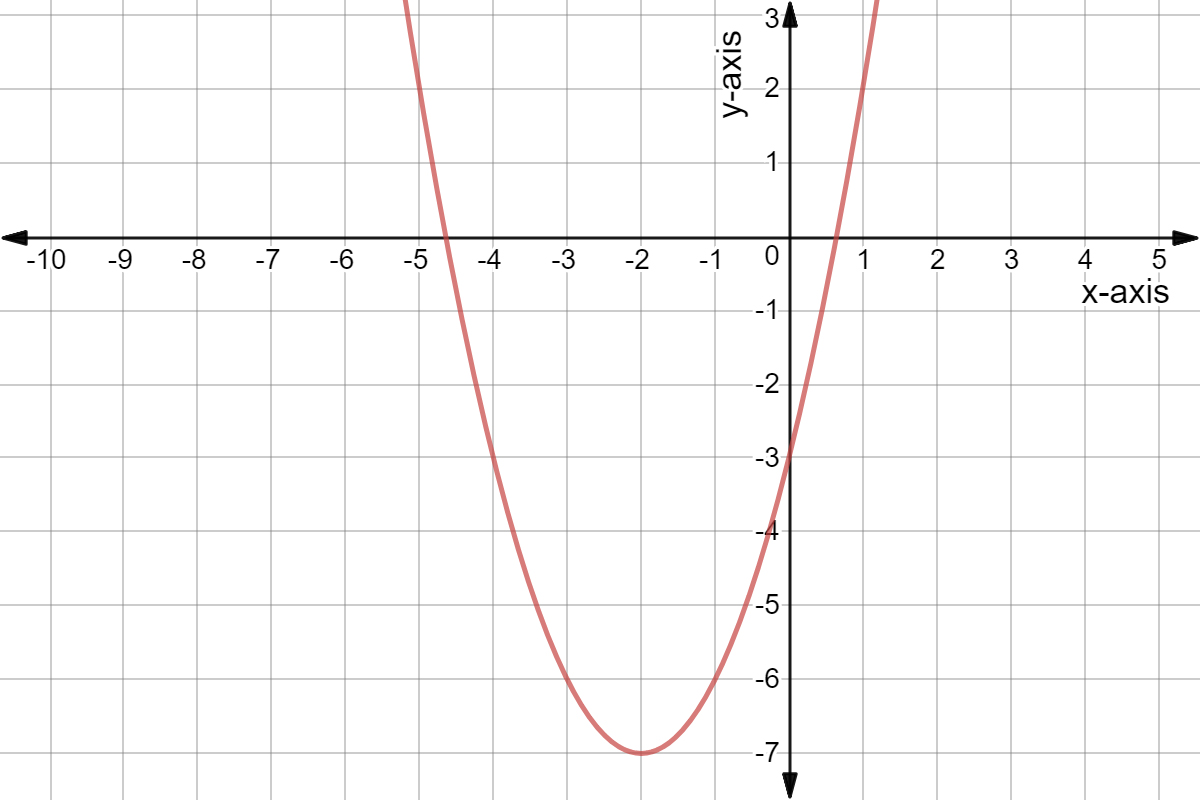
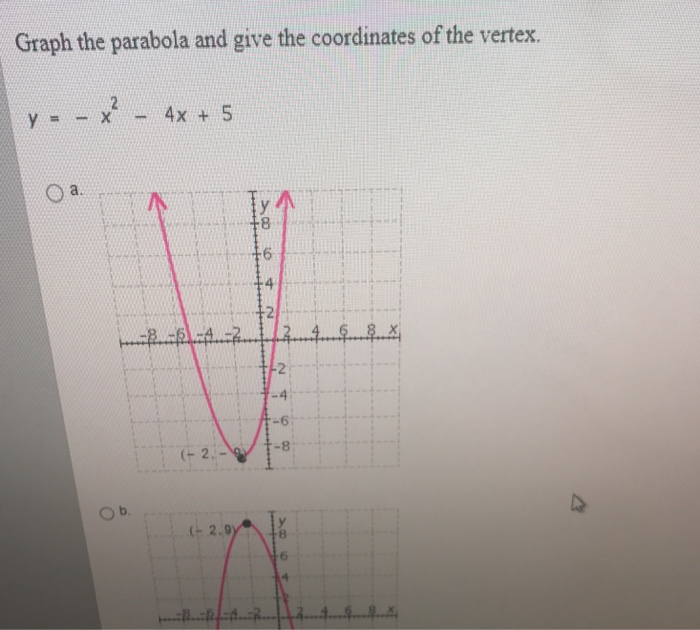
Find the coordinates of the vertex of the parabola whose equation is {eq}y = x^2 4x 3 {/eq} Given a quadratic function in vertex form, f(x) = We can use the process of Completing the Square to get this into the Vertex Form y = x2 − 4x 2 → y −2 = x2 − 4x (Transposed 2 to the Left Hand Side) Now we ADD 4 from each side to complete the square → y −2 4 = x2 − 4x 22 → y 2 = (x − 2)2 → y = 1 ⋅ (x −2)2 −2 is the Vertex Form The vertex of the Parabola is {2, −2}
Incoming Term: y=x^2-4x+1 vertex, y=x^2+4x-1 vertex form, write y=x^2+4x-1 in vertex form, find the vertex of y=x^2-4x-1,




0 件のコメント:
コメントを投稿